SciBase Journals
SciBase Dentistry and Oral Sciences
ISSN 2691-7785
- Article Type: Research Article
- Volume 1, Issue 1
- Received: Aug 11, 2023
- Accepted: Sep 07, 2023
- Published Online: Sep 14, 2023
Tissue Thermal Response in Photobiomodulation Therapy: A Theoretical Study
Parviz Parvin1*; Hamid Reza Dehghanpour1; Atefeh Bahrambeigi2; Pourandokht Davoudi2
1Physics Department, Amirkabir University of Technology, P.O. Box 15875-4413, Tehran, Iran.
2School of Density, Hamedan University of Medical Science, Hamedan, Iran.
*Corresponding Author: Parviz Parvin
Physics Department, Amirkabir University of Technology, P.O. Box 15875-4413, Tehran, Iran.
Email: parvin@aut.ac.ir
Abstract
The PBM treatment method is widely used in the treatment of oral and dental diseases, especially the fast treatment of aphthous. Although the conversion and distribution of laser beam energy in the form of heat is important, when the laser intensity is less than 500 mw/cm2, the photochemical reactions that occur simultaneously in the tissue environment are considered to be the dominant process compared to the thermal effects. Due to the insignificant increase in the temperature of the tissue, its experimental measurement is often accompanied by a significant error, and the use of a theoretical calculation method based on the solution of the heat transfer equation in the tissue environment can increase the accuracy in determining the temperature rising of the tissue. This can lead to the prediction of optimal irradiation conditions. Here, we have obtained the instantaneous temperature changes in the tissue by using the bio-heat equation and its numerical solution by the Gauss-Seidel method.
Keywords: Dental diseases; Treatment; Temperature.
Citation: Parvin P, Hamid Reza D, Atefeh B, Davoudi P. Tissue Thermal Response in Photobiomodulation Therapy: A Theoretical Study. SciBase Dent Oral Sci. 2023; 1(1): 1001.
Introduction
Photobiomodulation (PBM) is one of the non-invasive treatment technics using light sources that is carried out by biological activities in photochemical reactions. Photobiomodulation (PBM) deals with non-thermal laser-tissue interactions when low-level laser exposure is applied to the target tissue. The mechanism of PBM has already been reported [1,2]. The effect of PBM treatment has been reported on healing wounds, burns and reducing muscle and joint pain [3-6]. The interaction of photons with strongly scattering environments leads to back-scattering and multiple scattering, which causes deviation from the Lambert-Beer law. The result of this scattering is the accumulation of photons in the lower layers of the tissue [7].
In tissues where the absorption coefficient is significantly higher than the scattering coefficient, the Lambert-Beer law can be used. In PBM, due to the use of laser in the therapeutic window, the ratio of scattering to absorption coefficient is often much higher than 1, in other words, a correctional term that is a function of the scattering coefficient is added to the Lambert-Beer law. In this work, the heat transfer equation in the tissue is solved by the Green’s function method and it has been shown that the PBM raises the tissue temperature ~0.1°C.
Theory
Due to the low laser intensity, heat transfer parameters and tissue optical coefficients can be assumed to be constant and independent of temperature. In the mathematical model, a semiconfined homogeneous environment is exposed to continuous laser radiation with a Gaussian radial laser beam, and the thermal coefficients of the tissue are assumed to be almost similar to water parameters. The thermal and optical parameters of the tissue are determined for the wavelength of 810 nm. Calculations are performed in a cylindrical coordinate system. Then, the instantaneous temperature profile is determined. The temperature behavior of biological tissue is written by the bioheat equation as follows:
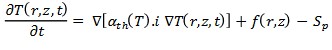
When the diffusion rate of blood in the target tissue is small, the expression of heat extraction through blood circulation, Sp, can be ignored and thus the bioheat equation becomes the heat transfer equation. Where, 𝛼𝑡ℎ = 𝐾p/c and K, 𝜌 and C are the heat transfer coefficient, density and heat capacity of the tissue, respectively. f(r,z) represents the source function and q = ρCf(w/cm2) represents the volumetric power of the thermal source caused by the photon absorption process in the optical interaction of the laser light with the biological tissue. Usually, the source expression according to the penetration depth is as follows [8]:
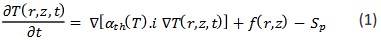
Where 𝜇𝑡 = 𝜇𝑎 + 𝜇𝑠 while 𝜇𝑎 and 𝜇𝑠 are absorption and scattering coefficient, respectively. 𝐼0 is the central intensity of the
laser beam, which decreases radially as exp [−2 ]. f(us) is the source correction function for deviations from the Lambert-Beer law in strongly scattering environments in the therapeutic
window region. ro is defined as the effective radius of the laser
beam so that the intensity is equal to the central intensity of the
beam and R represents the direct reflection coefficient from the
tissue surface.
In PBM, assuming that heat transfer coefficients are temperature independent, the temperature is as follow:
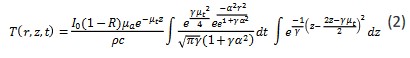
Where 𝜇𝑡 = 𝜇𝑎 + 𝜇𝑠, 𝛼 = 2 is the laser cutoff time.
If the medium is assumed to be completely absorbing (𝜇𝑠 → 0, 𝜇𝑎 → ∞), equation (1) becomes:
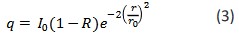
In this case, equation (2) becomes simpler:
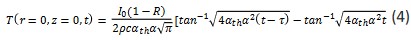
When τ → ∞ and just at the time of laser cutoff, equation (2) becomes its simplest form:
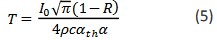
Equation (5) implies that the temperature will not exceed an upper limit. For a real environment, the upper limit of temperature will be lower than the value of equation (5).
In our model, tissue is assumed to be an environment with 70% water and its optical and thermal coefficients are given in Table 1
Results & discussion
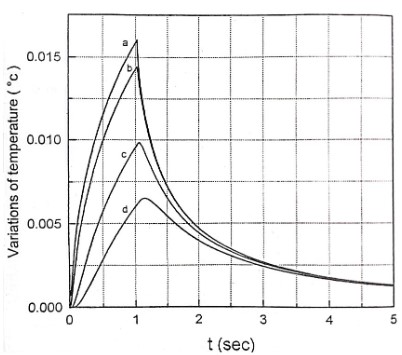
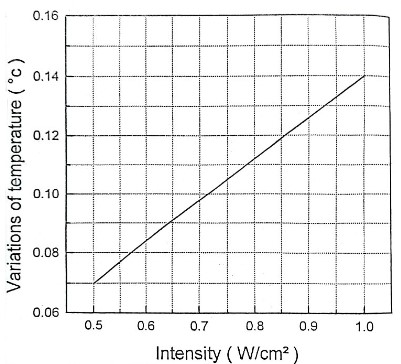
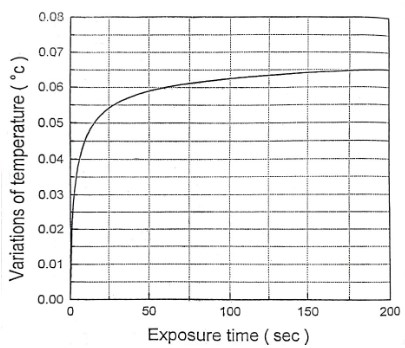
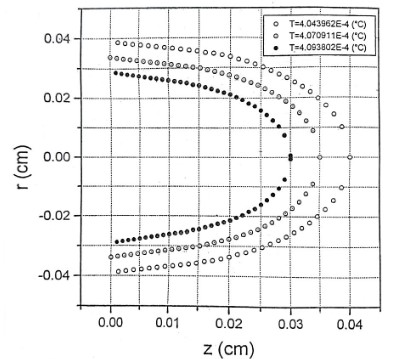
Here, we expose the tissue to the radiation of a He-Ne laser with a power of 20 mW. The beam diameter and intensity are assumed to be 0.225 cm and 500 mW/cm2 respectively. The heat transfer equation was solved by finite difference numerical technique and using Gauss-Seidel method. In figure 1 thermal responses at r = 0 for 1 second irradiation time and at laser penetration depths of 0, 0.013, 0.026 and 0.039 cm are shown. The temperature increase as a non-linear function of the irradiation time. This temperature rise is remarkably fast in the first second of irradiation. After stopping the radiation, the temperature has a significant rapid drop so that after the third second of irradiation, it tends to zero asymptotically, independent of the beam penetration depth. Normal body temperature is 36.5°C. When the temperature reaches more than 40°C, the gradual change of the protein from the normal state occurs and this leads to the local destruction of the tissue. Since BMP does not increase the temperature of the tissue locally, it does not cause thermal destruction of the tissue. The results of the figure 1 are a good confirmation of this issue, because the maximum for tissue temperature increase is 0.015°C. Temperature variation according to different radiation intensities for 1h irradiation time is shown in Figure 2. As can be seen, this correlation is linear. A 0.14°C temperature rising is predicted for the maximum laser intensity of 1 W/cm2. The temperature increase as a non-linear function of the irradiation time. This temperature rise is remarkably fast in the first 25 seconds of irradiation. These confirm the greater penetration depth of the beam for longer irradiation times. The mentioned topics can be concluded from Figure 3. Figure 4 shows isothermal contours for an irradiation time of 1s and at the exact moment of observation equal to 𝜏. Average speed of heat diffusion and temperature gradient can be determined using these isothermal curves. By simultaneously using the results of figures 1-4, it is possible to determine the optimal conditions of BMP treatment. Based on these calculations, only one percent of the laser beam energy has been converted into heat, and most of this energy contributes to the acceleration of photochemical reactions. The photons stimulate the mitochondria of the cells, which lead to the release of neurotransmitters such as enkephalin and epinephrine. As a result, anti-inflammatory and pain-relieving effects are observed in the human body.
Table 1: Frontal CT scan showing the mass an upper polar tissue mass of the left kidney.
| Symbol | ||
|---|---|---|
| Thermal diffusivity | 𝛼𝑡ℎ | 0.00115 cm2/S |
| Thermal conductivity | K | 0.0042 W/ cm2o C |
| Heat capacity | c | 3.35 J/go C |
| Density | 𝜌 | 1.09 g/cm3 |
| Absorption | 𝜇𝑎 | 2 cm-1 |
| Diffusion Coefficient | 𝜇𝑠 | 188 cm-1 | Reflection | R | 5% |
Conclusion
Here, a fast and reliable solution for the heat transfer equation for low-power laser irradiation on tissue was presented using the Green’s function method. This solution confirms the slight increase in tissue temperature and the non-destructive effects of laser therapy. The results obtained from this simulation can be effectively used in determining the treatment protocol with the BMP method using isothermal contours evaluation in determining the range of laser intensity. On the other hand, it is also possible to determine the appropriate values for the duration of irradiation and the intensity of the incident beam to determine the conditions of the treatment at the surface or depth of the tissue.
References
- Hamblin M, Demidova T. Mechanisms of Low Level Light Therapy. Proc. of SPIE. 2006; 6140: 614001.
- Hamblin M. Photobiomodulation or low-level laser therapy, J. Biophotonics. 2016; 9: 1122–1124.
- Dehghanpour HR, Parvin P, Ganjali P, Golchini A, Eshghifard H, et al. Evaluation of Photobiomodulation effect on cesarean-sectioned wound healing- A clinical study, Due to Publish in Lasers in Medical Science. 2023.
- Mokmeli S, Khazemikho N, Niromanesh S, Vatankhah Z. The application of low-level laser therapy after cesarean section does not compromise blood prolactin levels and lactation status. Photomed. Laser Surg. 2009; 27: 509–512.
- de Holanda Araujo A M P, de Sena K R R, da Silva Filho E M, Pegado R, Micussi M T A B C. Low-level laser therapy improves pain in postcesarean section: a randomized clinical trial. Lasers Med. Sci. 2020; 35: 1095–1102.
- Poursalehan S, Nesioonpour S, Akhondzadeh R, Mokmeli S. The Effect of Low-Level Laser on Postoperative Pain After Elective Cesarean Section. Anesth. Pain. Med. 2018; 8: e84195.
- Parvin P, Eftekharnoori S, Dehghanpour HR. Monte Carlo simulation of photon densities inside the dermis in LLLT (Low Level Laser Therapy). Opt. Spectrosc. 2009; 107: 489.
- Ball C S, Sepko KA, Jacob LJ. Thalidomide for treatment of oral aphthous ulcers in patients with HIV. AJG. 1997; 92: 169-170.